HihoCoder – 1511 树的方差 无根树的计数、分配式方差、分数取模

树的方差 无根树的计数、分配式方差、分数取模

Source

HihoCoder - 1511

My Solution

题意：给出一个n，表示n个节点的无根树，每个节点的权值是deg[i]即节点的度，求所有 节点个数为n的无根树的deg[i]方差 的和。

无根树的计数、平均方差、分数取模

首先要用到一个分配式方差公式(笔者自己命的名),

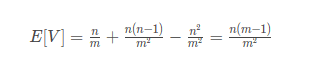
表示把n个东西分配成m分时的方差。

这里长度为n的无根树，则sigma{deg[i]} == 2*(n-1)。

然后点的度数必定大于0，所以 相当于把 2*(n-1) - n 个东西分配成 n 份的方差 的和。

这里节点数为n的完全图有 n^(n-2) 种无根树，

所以答案是 (n-1)*(n-2) / (n^2) * n ^ (n-2) == (n-1)*(n-2) * n ^(n-4)，

然后对n讨论， n >= 4 的时候直接快速幂，小于4的时候应用分数取模==分子*(分母的逆元)。

官方题解给出了一些证明

复杂度 O(1)

#include 
#include 
#include 
using namespace std;
typedef long long LL;
const int MAXN = 2e5 + 8;
const LL MOD = 998244353;

string s;

inline LL mod(LL a)
{
    return a - a / MOD * MOD;
}

inline LL pow_mod(LL a, LL i)
{
    if(i == 0) return mod(1);
    LL t = pow_mod(a, i>>1);
    t = mod(t * t);
    if(i & 1) t = mod(t * a);
    return t;
}

inline LL get(LL a)
{
    return pow_mod(a, MOD - 2);
}

int main()
{
    #ifdef LOCAL
    freopen("c.txt", "r", stdin);
    //freopen("c.out", "w", stdout);
    int T = 4;
    while(T--){
    #endif // LOCAL
    ios::sync_with_stdio(false); cin.tie(0);

    LL n, ans = 0;
    cin >> n;
    ans = mod((n-2)*(n-1));
    if(n >= 4){
        ans = mod(ans*pow_mod(n, n - 4));
    }
    else{
        ans = mod(ans * get(pow_mod(n, 4 - n)));
    }
    cout << ans << endl;


    #ifdef LOCAL
    cout << endl;
    }
    #endif // LOCAL
    return 0;
}

非特殊说明，本博所有文章均为博主原创，未经许可不得转载。

https://www.prolightsfxjh.com/

Thank you!

                                                                                                                                             ------from ProLightsfx