My Solution
题意:给出一个只有"("和“)"的字符串,为有多少个子序列,它的长度为len,则左边len/2个字符为”("右边len/2个字符为")",问这样的子序列有多少个。
前缀的后缀、 范德蒙恒等式、容斥
子串为 前缀的后缀,这里是子序列,所以s[i]为必取,作为序列的最后一个元素,然后前面的"("为选取,
所以可以预处理出suml和sumr,分表表示i的左边有多少个"(", i的右边有多少个")".
然后对于每个“(",必选这一个"(",然后i之前的(进行排列组合,选j个"(",就在sumr[i+1]里选j个")"。
所以就是sigma{C(a, j) * C(b, j)},然后这里恰好有个叫做范德蒙恒等式的公式,
然后根据上面所描述的方法,每次i是必选的,然后进行排列组合。
ans += C(suml[i] + sumr[i+1, suml[i]) - C(suml[i-1] + sumr[i+1], suml[i-1]);
复杂度 O(nlogn)
#include
#include
#include
using namespace std;
typedef long long LL;
const int MAXN = 2e5 + 8;
const LL MOD = 1e9 + 7;
LL suml[MAXN], sumr[MAXN], fac[MAXN];
string s;
inline LL mod(LL a)
{
return a - a / MOD * MOD;
}
inline LL pow_mod(LL a, LL i)
{
if(i == 0) return mod(1);
LL t = pow_mod(a, i>>1);
t = mod(t * t);
if(i & 1) t = mod(t * a);
return t;
}
inline LL get(LL a,LL b)
{
return mod(fac[a+b] * pow_mod(mod(fac[a] * fac[b]), MOD - 2));
}
int main()
{
#ifdef LOCAL
freopen("d.txt", "r", stdin);
//freopen("d.out", "w", stdout);
int T = 4;
while(T--){
#endif // LOCAL
ios::sync_with_stdio(false); cin.tie(0);
cin >> s;
int sz = s.size(), i;
fac[0] = 1;
for(i = 1; i <= sz; i++) fac[i] = mod(fac[i-1] * i);
for(i = 0; i < sz; i++){ if(i == 0){ suml[i] = 0; if(s[i] == '(') suml[i] += 1; } else{ suml[i] = suml[i-1]; if(s[i] == '(') suml[i] += 1; } } sumr[sz] = 0; for(i = sz - 1; i >= 0; i--){
sumr[i] = sumr[i+1];
if(s[i] == ')') sumr[i] += 1;
}
LL ans = 0;
for(i = 0; i < sz; i++){
if(s[i] == '('){
ans = mod(ans + get(suml[i], sumr[i+1]) - get(suml[i-1], sumr[i+1]) );
}
}
while(ans < 0) ans += MOD;
cout << ans << endl;
#ifdef LOCAL
cout << endl;
}
#endif // LOCAL
return 0;
}
非特殊说明,本博所有文章均为博主原创,未经许可不得转载。
https://www.prolightsfxjh.com/
Thank you!
------from ProLightsfx
非特殊说明,本博所有文章均为博主原创,未经许可不得转载。
如经许可后转载,请注明出处:https://prolightsfxjh.com/article/codeforces-round-404-div-2-d-anton-and-school-2/

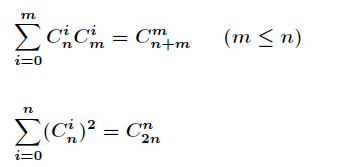






共有 0 条评论