Codeforces Round #397 (Div. 1 + Div. 2 combined) D. Artsem and Saunders 映射+构造

My Solution

题意：给出一个函数f(x) 属于[1,x]，然后要求确定一个数m，使x属于[1,n]，g[x]属于[1,m], x输入[1,m] h[x]属于[1,n], 当存在m时，求m最小时的gx和hx。

映射+构造

先把fx离散化化，然后通过离散化的结果，和h(g(x)) = f(x) for all

, 求出gi 和 hi，

最后用g(h(x)) = x for all

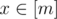
来检查gi和hi，如果可以则输出，否则-1.

其中可以证明 fi 离散化成任意[1,m]都不影响结果，只要保证不同的数离散化成不同的数，相同的数离散化成相同的数即可。

复杂度 O(n)

#include 
#include 
#include 





using namespace std;
typedef long long LL;
const int maxn = 1e5 + 8;

int f[maxn], g[maxn], h[10*maxn];
map<int, int> mp, mpp;

int main()
{
    #ifdef LOCAL
    freopen("d.txt", "r", stdin);
    //freopen("d.out", "w", stdout);
    int T = 4;
    while(T--){
    #endif // LOCAL
    ios::sync_with_stdio(false); cin.tie(0);

    int n, i, j = 1, m;
    cin >> n;
    for(i = 1; i <= n; i++) {cin >> f[i]; mp[f[i]]++;}
    m = mp.size();
    for(auto k = mp.begin(); k != mp.end(); k++){
        mpp[k->first] = j; j++;
    }
    for(i = 1; i <= n; i++){
        g[i] = mpp[f[i]];
        h[mpp[f[i]]] = f[i];
    }
    bool ans = true;
    for(i = 1; i <= m; i++){
        if(g[h[i]] != i) ans = false;
    }
    if(ans){
        cout << m << "n";
        cout << g[1]; for(i = 2; i <= n; i++) cout << " " << g[i];
        cout << "n" << h[1]; for(i = 2; i <= m; i++) cout << " " << h[i];
        cout << endl;
    }
    else cout << -1 << endl;


    #ifdef LOCAL
    mp.clear(); mpp.clear();
    cout << endl;
    }
    #endif // LOCAL
    return 0;
}

非特殊说明，本博所有文章均为博主原创，未经许可不得转载。

https://www.prolightsfxjh.com/

Thank you!

------from ProLightsfx

Codeforces Round #397 (Div. 1 + Div. 2 combined) D. Artsem and Saunders 映射+构造

相关推荐

UESTC 1705 咸鱼钟大爷随机化+哈希

Gym – 101102J J. Divisible Numbers 位运算+优化+前缀和

Gym 100541 D. Treasure Box 循环(散乱的前缀+循环体)

Codeforces Round #364 (Div. 2) D. As Fast As Possible __ binary search、方程或解方程直接解出答案

共有 0 条评论

公告

游戏服务器开发 最新文章

1转行游戏开发第二年，开始修炼内功

2搜撤类游戏全服装备防复制方案

3从通用后台开发到游戏服务器开发...

公众号

推荐系统开发 最新文章

1时序数据库与NB时序特征

2从零搭建NB特征平台

3NB特征分类标准

4浅谈NB推荐系统架构-ProLightsfx

5一次推荐系统线上事故的排查与修...

标签云

栏目分类

Codeforces Round #397 (Div. 1 + Div. 2 combined) D. Artsem and Saunders 映射+构造

相关推荐

UESTC 1705 咸鱼钟大爷 随机化+哈希

Gym – 101102J J. Divisible Numbers 位运算+优化+前缀和

Gym 100541 D. Treasure Box 循环(散乱的前缀+循环体)

Codeforces Round #364 (Div. 2) D. As Fast As Possible __ binary search、方程 或解方程 直接解出答案

共有 0 条评论

公告

游戏服务器开发最新文章

1转行游戏开发第二年，开始修炼内功

2搜撤类游戏全服装备防复制方案

3从通用后台开发到游戏服务器开发...

公众号

推荐系统开发最新文章

1时序数据库与NB时序特征

2从零搭建NB特征平台

3NB特征分类标准

4浅谈NB推荐系统架构-ProLightsfx

5一次推荐系统线上事故的排查与修...

标签云

栏目分类

UESTC 1705 咸鱼钟大爷随机化+哈希

Codeforces Round #364 (Div. 2) D. As Fast As Possible __ binary search、方程或解方程直接解出答案